DiffAnt: Diffusion Models for Action Anticipation

¹KIT IAR-IES, ²Fraunhofer IOSB, ³University of Bonn IAI

Abstract

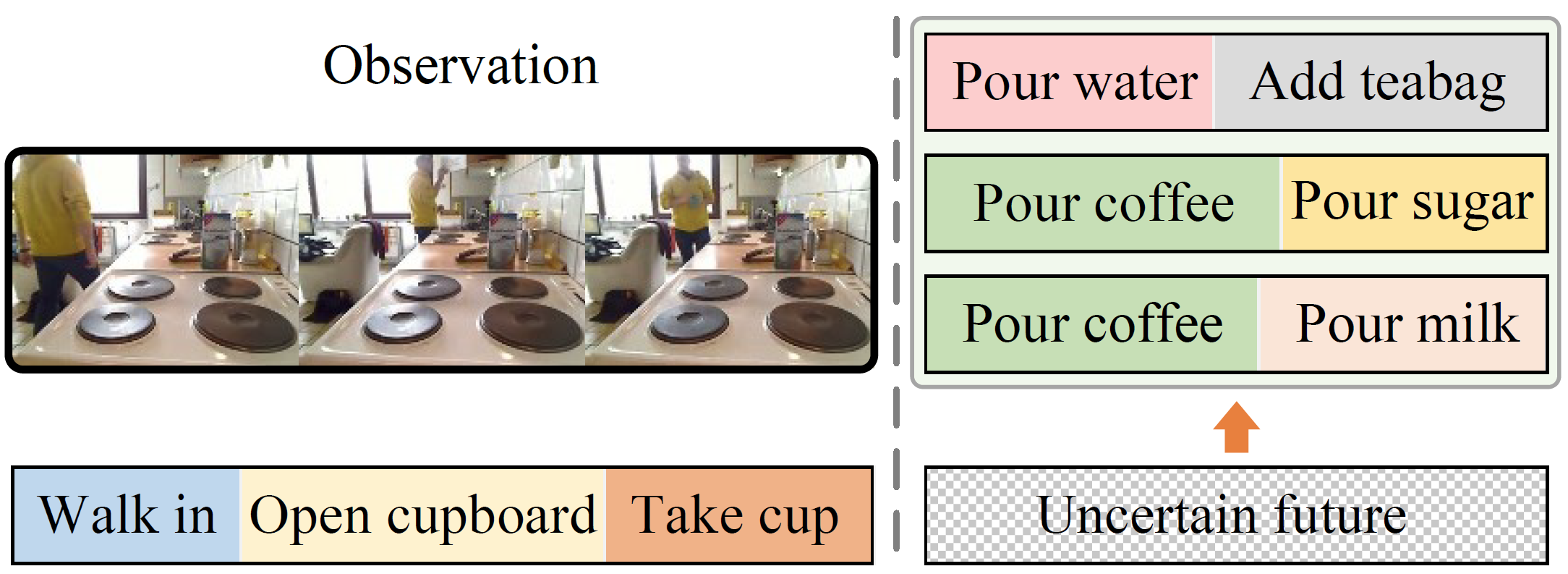
Anticipating future actions is inherently uncertain. Given an observed video segment containing ongoing actions, multiple subsequent actions can plausibly follow. This uncertainty becomes even larger when predicting far into the future. However, the majority of existing action anticipation models adhere to a deterministic approach, neglecting to account for future uncertainties. In this work, we rethink action anticipation from a generative view, employing diffusion models to capture different possible future actions. In this framework, future actions are iteratively generated from standard Gaussian noise in the latent space, conditioned on the observed video, and subsequently transitioned into the action space. Extensive experiments on four benchmark datasets, i.e., Breakfast, 50Salads, EpicKitchens, and EGTEA Gaze+, are performed and the proposed method achieves superior or comparable results to state-of-the-art methods, showing the effectiveness of a generative approach for action anticipation.

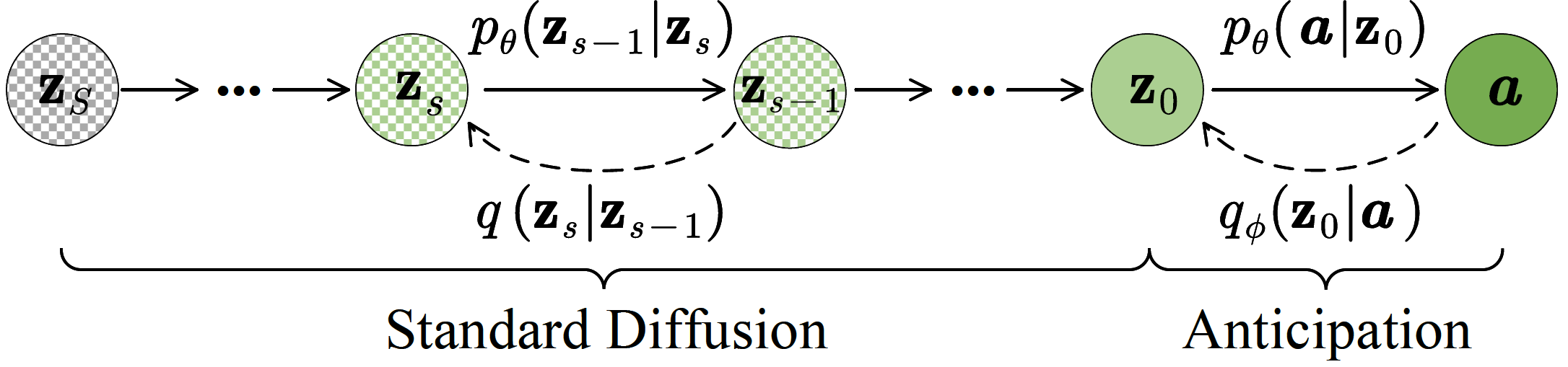
Overall Inference Pipeline

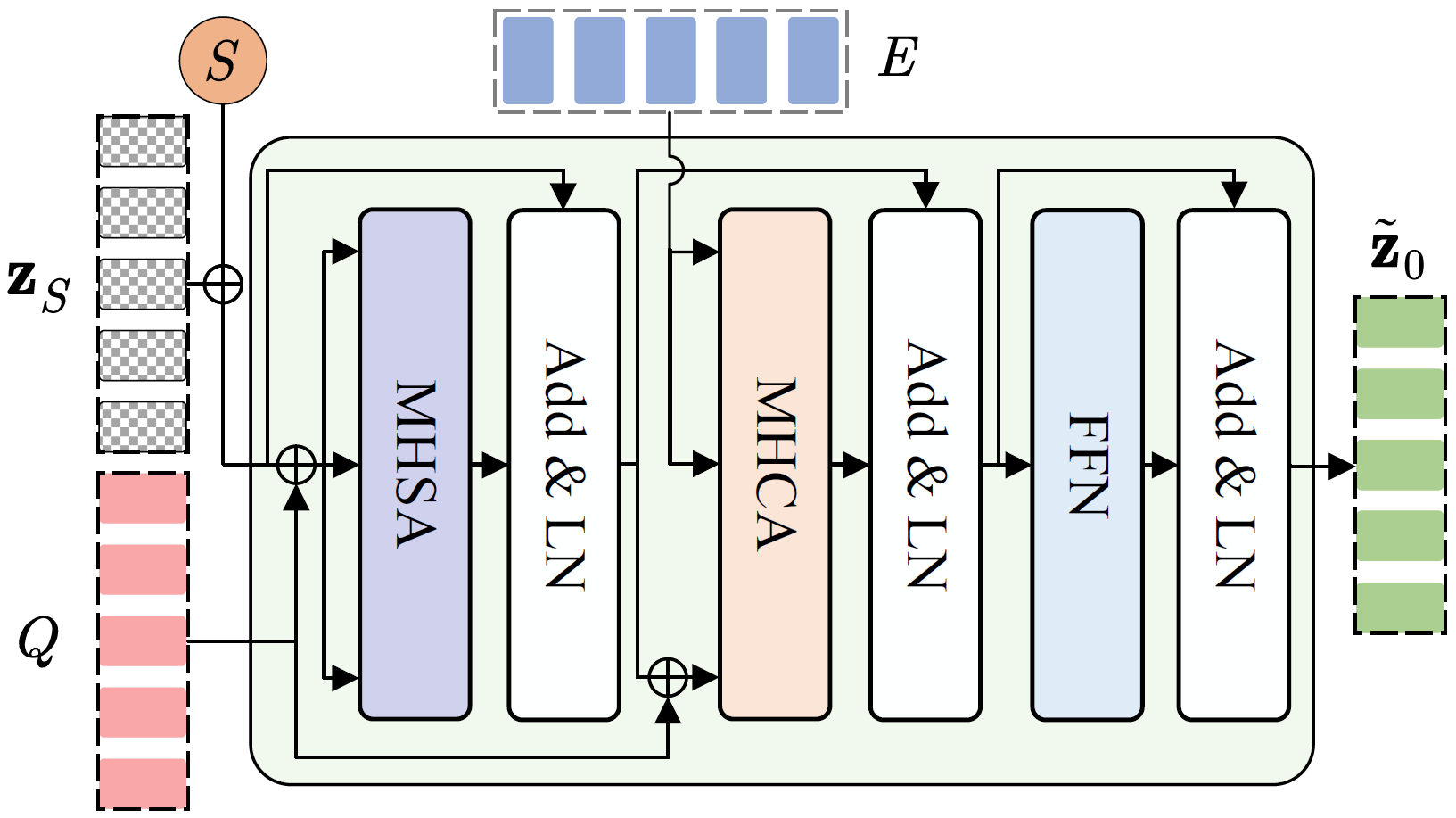
During inference, future action embeddings \( \mathbf{z}_S \) are drawn from a standard Gaussian distribution \( \mathcal{N} \) ( \( \boldsymbol{0} \), \( \boldsymbol{I} \) ). Alternatively, we can initialize \( \mathbf{z}_S \) with zero vectors (mean of the standard Gaussian distribution) for deterministic results. The decoder is made step-aware by embedding the current diffusion step \( s=S \) with sinusoidal positional encodings, futher integrated via a multi-layer perceptron. The decoder inputs \( \mathbf{z}_S \), \( Q \), and step data, aiming to initially rectify the noisy futures and predict \( \tilde{\mathbf{z}}_0 \), taking cues from the encoded past observations \( E \) via cross-attention. To enable the iterative reverse diffusion process, we apply the forward chain to get \( \tilde{\mathbf{z}}_{S-1} \) and input it with the updated step \( s=S-1 \) to the decoder. By iteratively removing noise, a final sample \( \tilde{\mathbf{z}}_0 \) is generated via a trajectory \( \mathbf{z}_{S} \), \( \tilde{\mathbf{z}}_{S-1} \), ..., \( \tilde{\mathbf{z}}_0 \).

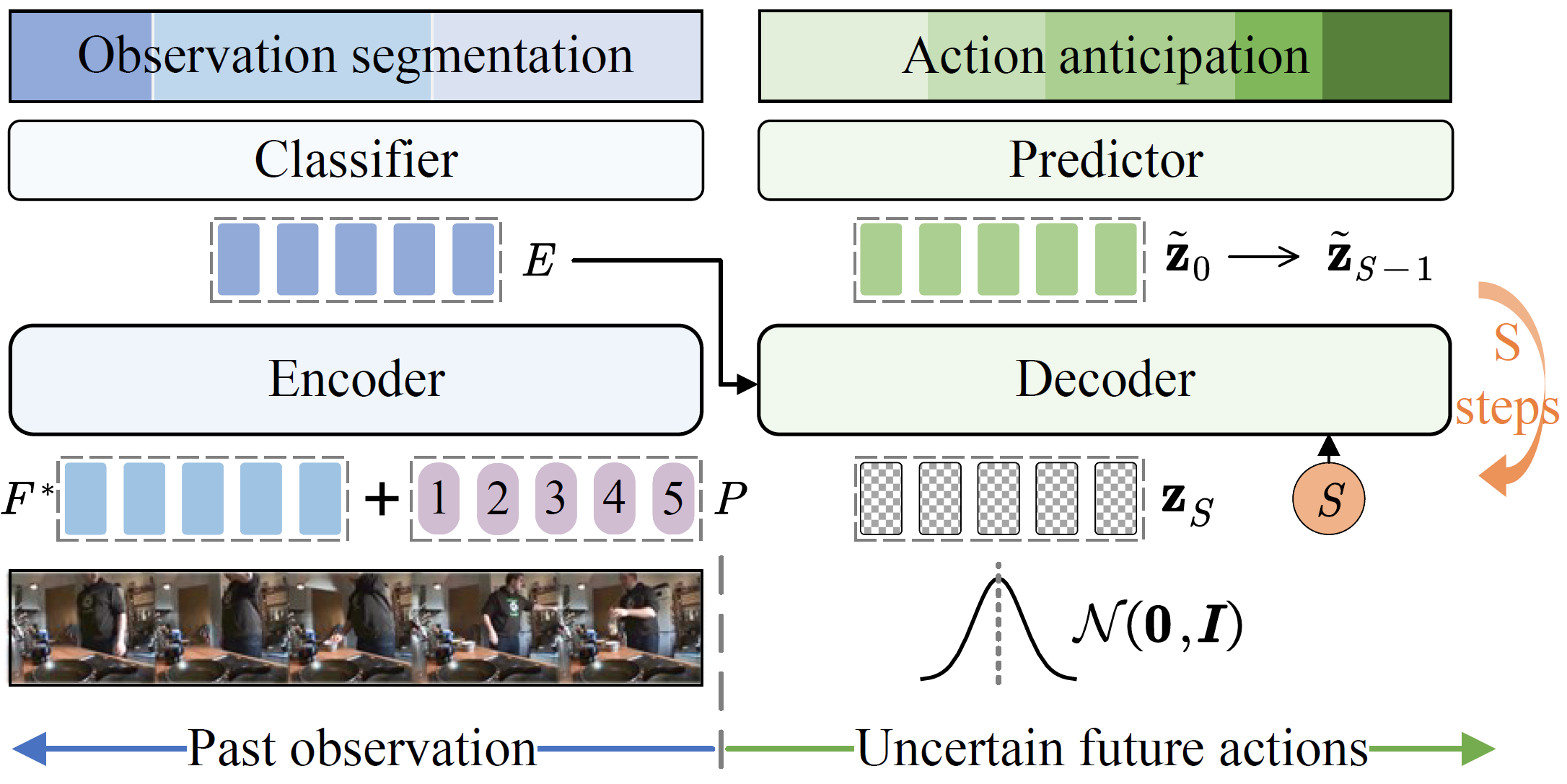
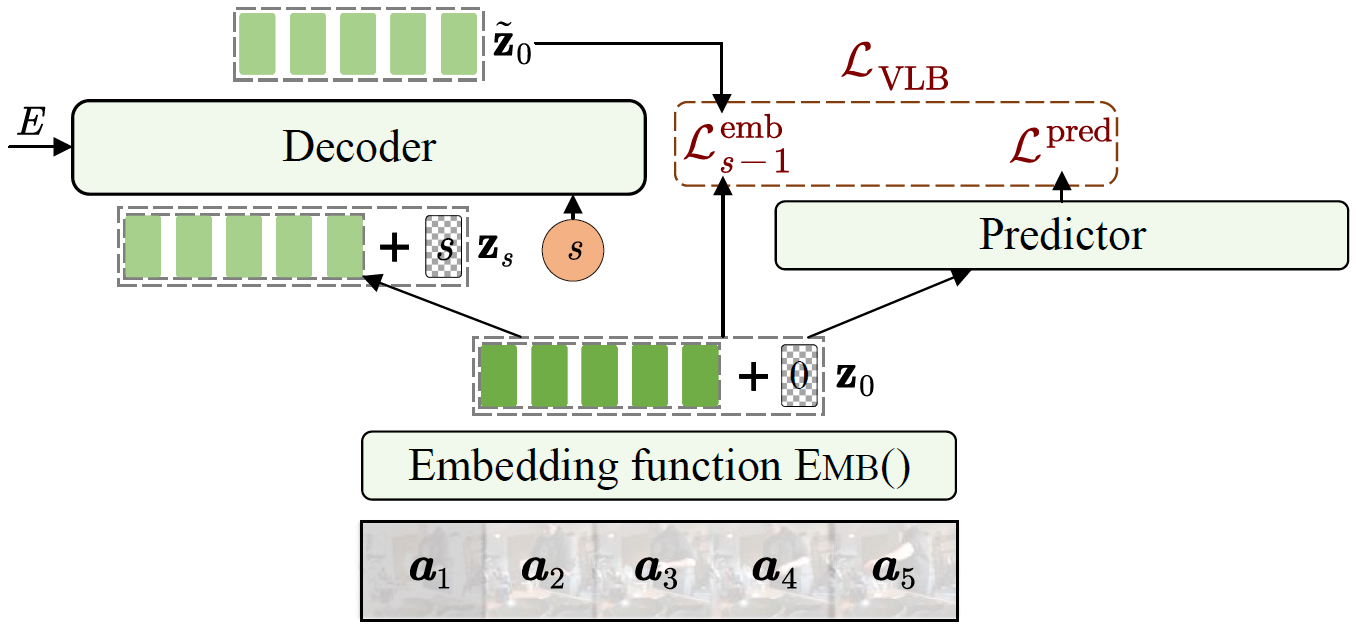
Training

To integrate discrete actions \( \boldsymbol{a} \) into the continuous diffusion processes, we extend standard diffusion models with a future action embedding function and an action predictor to facilitate the conversion between continuous embeddings \( \mathbf{z}_0 \) and discrete actions \( \boldsymbol{a} \).

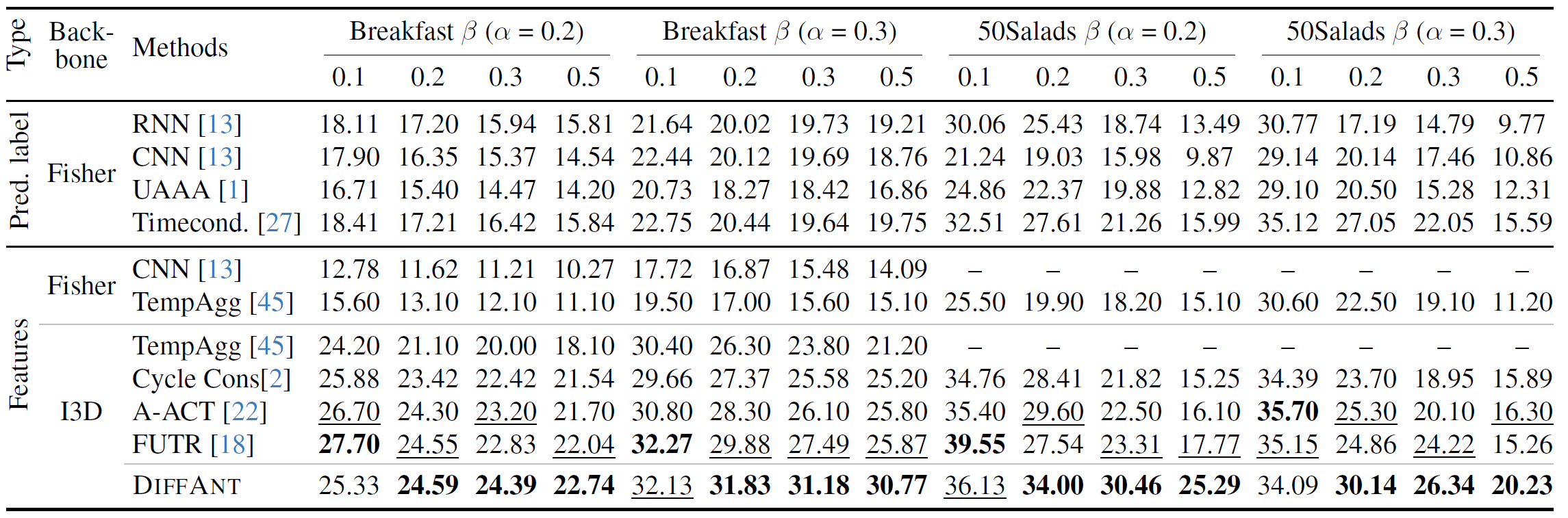
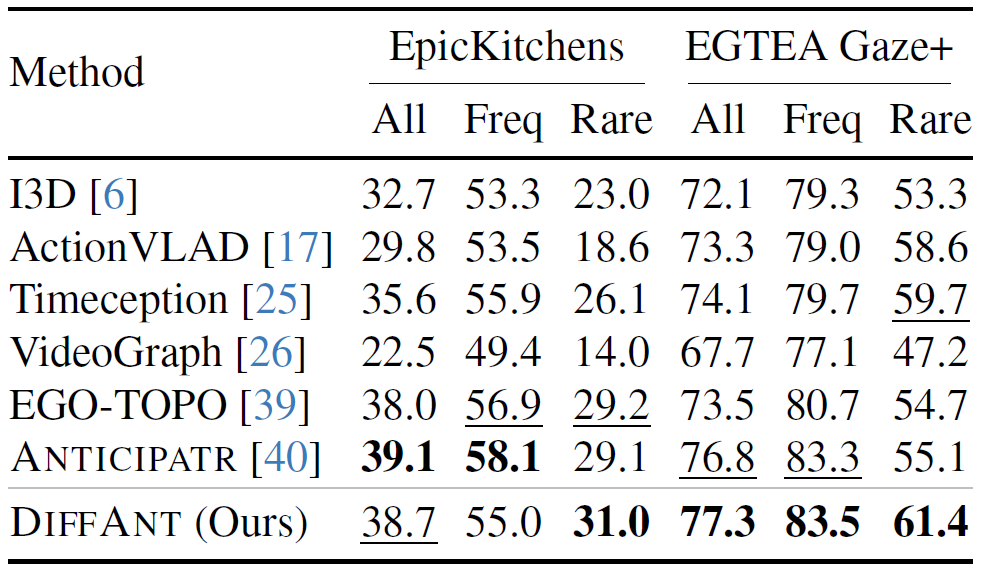
Quantitative Results

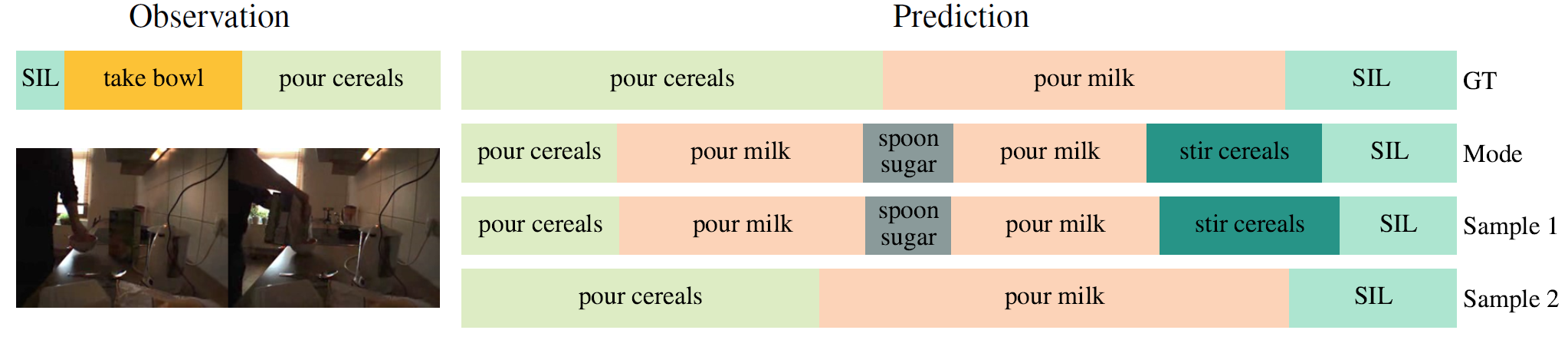
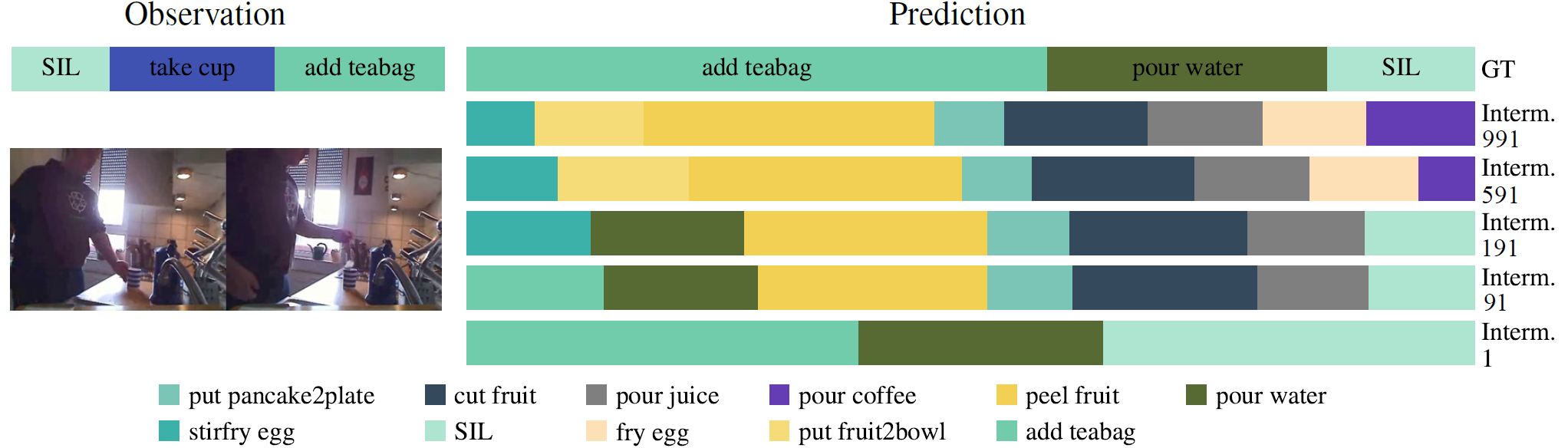
Qualitative Results